老生常谈，JS中数学计算精度问题的解决方案

wyh 2023/12/1

# 故事从0.1+0.2说起

0.1+0.2是否等于0.3呢?

这是一个前端人耳熟能详的故事，每一个初入前端世界的人，应该都会被它来一次灵魂拷问。它的出现，似乎打破了人们以往对于代码世界“执行严谨、一丝不苟”的刻板印象。然而，这看起来“不够严谨”的形成原因，却正是因为底层代码执行的足够严谨！

在初入前端世界的时候，有那么一瞬，我甚至在想难道是底层对于0.1和0.2有一种特殊的感情？

然而事实并非如此，能被底层这种庞然大物看上并针对的，当让不会只有0.1和0.2这两个看起来平平无奇的数字，而是包含了这两个数字在内的一批特殊存在。

如下图所示：

当然，除上述图片内的数字之外，还有更多的其他数字也在这反常理的队列之内。

然而，这篇文章我们并不是来深入讨论这些特殊的数字在进行数学计算时，与底层究竟产生了什么样的恩怨纠葛。我们只需要简单知道：在计算机世界中，所有信息最后都是以二进制存储的，可是数字中的小数部分在按照一定规则转换为二进制时，有些数字会产生无限循环的现象，但计算机精度位数是有限的，所以对超出位数的部分做了四舍五入的计算，因此造成了精度的丢失。

本文仅仅针对以上现象，结合日常开发的实践，讨论一些解决问题的方法。

# 初步解决

既然是因为小数部分在转换二进制时做了四舍五入的处理，那么计算时先将小数转为整数再计算是不是就可以了？

依据上面的思想，在javascript中进行小数计算，通常会采用放大倍数取整之后再计算，得出结果之后再缩小还原的技术方案。

例：计算0.1+0.2，通常会将0.1和0.2放大10倍，相加之后再缩小10倍

代码如下：

  /**
   * 已知：a为0.1，b为0.2
   * 求：a与b的和
   * */
  const a = 0.1;
  const b = 0.2;
  const result = ((a * 10) + (b * 10)) / 10;
  console.log(result) // 0.3

如上，针对已知小数位数的数字，我们可以直接采用放大相应倍数取整，然后再计算的方式来规避小数计算的精度问题。

可是在实际的业务开发中，对于需要进行计算处理的数字，我们往往无法预先获知数字包含的小数位数。对于此种情况，我们便需要先确定小数位数，然后确定放大倍数，再进行计算。

代码如下：

  /**
   * 已知：a，b为两个精度随机的小数
   * 求：a与b的和
  */

  // 生成精度随机的小数
  const getNumber = () => {
    const len = Math.random() * 10;
    const num = Number((Math.random() * 10).toFixed(len))
    return num
  }

  // 计算放大倍数
  const getPower = (a, b) => {
    // 获取a,b小数位长度，如没有小数位则默认值为0
    const aLen = a.toString().split(".")[1]?.length || 0;
    const bLen = b.toString().split(".")[1]?.length || 0;
    // 获取最大长度
    const len = Math.max(aLen, bLen);
    // 计算返回放大倍数
    return Math.pow(10, len)
  }

  const a = getNumber();
  const b = getNumber();
  const power = getPower(a, b);

  const result = ((a * power) + (b * power)) / power;

因为以上代码中，a和b皆由getNumber函数随机生成，为了便于观察，我们添加log后，在浏览器中运行代码。

如下图所示：

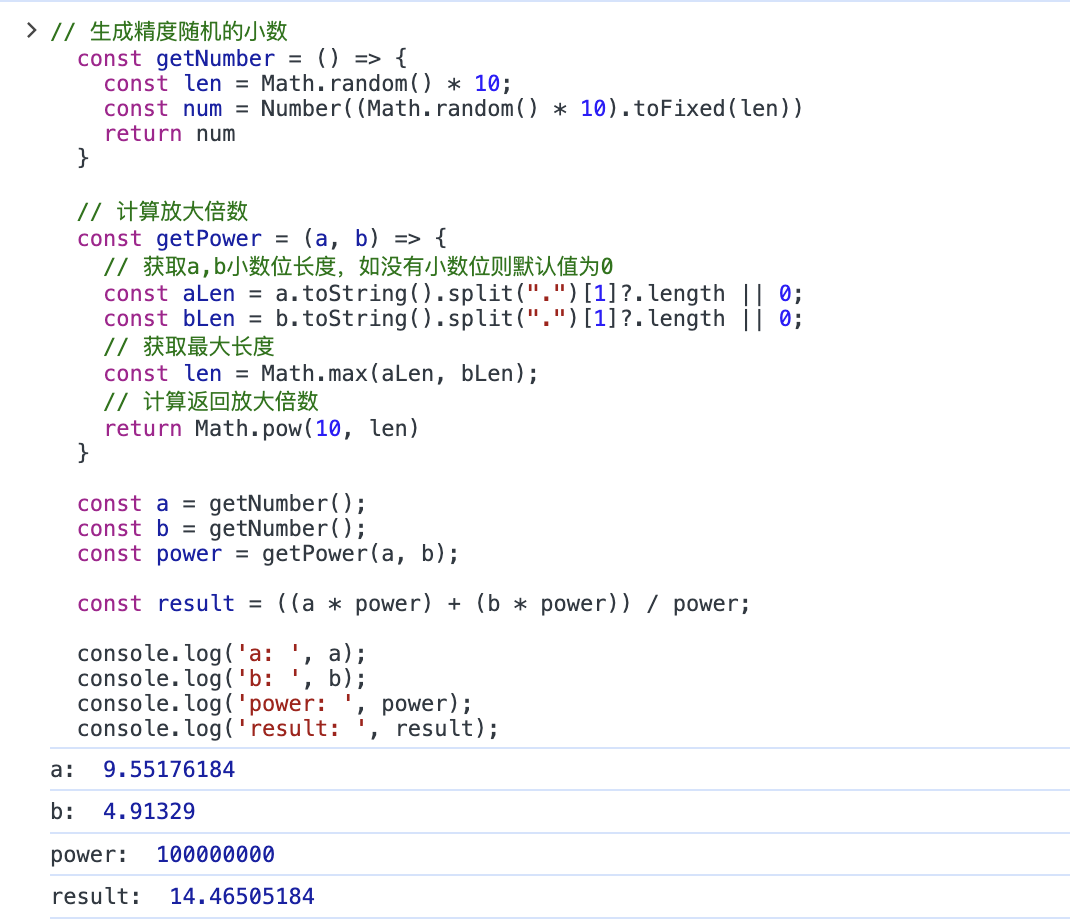
观察可知，计算结果正确。以上，我们通过使用getPower函数确定放大的倍数，然后进行计算。这也是目前大部分同学解决小数计算精度问题的主要方式。

然而，故事到这里就结束了吗？

当然不是！

以上方式虽然解决了一些精度问题，但是并没有解决所有的精度问题。在这个特殊的小数群体中，并不是所有的小数都可以通过放大倍数来取整的！

如下图所示：

因此先放大再计算也并不是十分可靠，如下图所示：

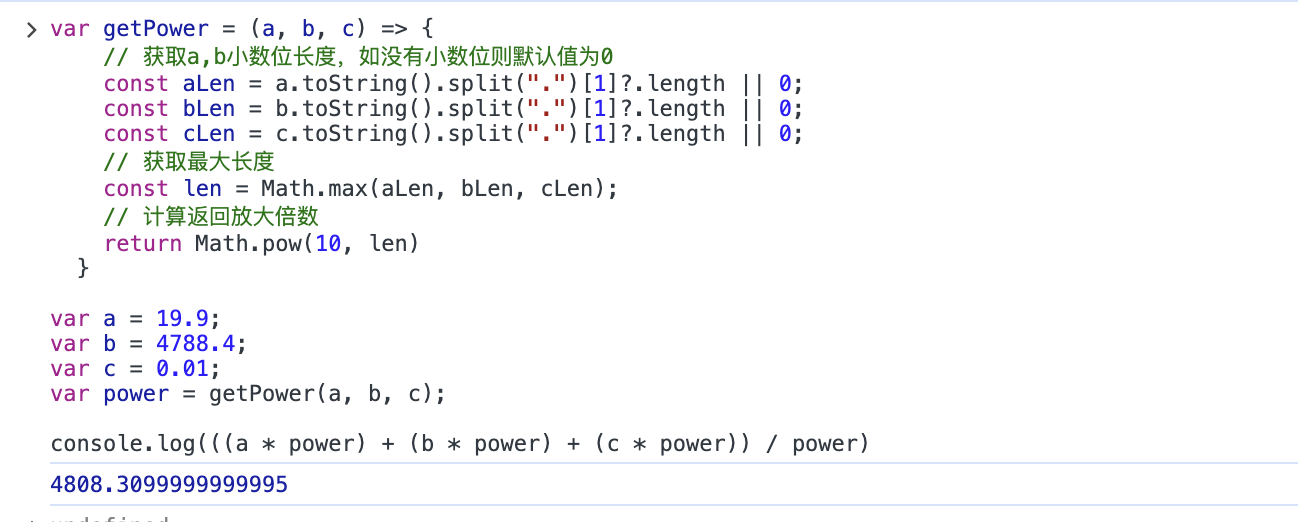
# 大胆取舍

# Number.EPSILON

我们已经知道，精度的误差是由于底层在计算时做了一些四舍五入造成的，因此我们分析后可以断定被舍弃的部分一定是小于可以表示的最小浮点数的。

例如：有数字 a 为 1.234，对 a 做保留两位小数的处理后，得到数字 b ，b的值为1.23。则上述操作中舍弃的部分 0.004，一定小于保留精度 0.01

基于以上分析，我们有理由相信：在 javascript 中当两个数字之间的差值小于可以表示的最小浮点数，那么我们就认为这两个数字相等。

可是，最小的浮点数该如何获取呢？

javascript 为我们提供了这样一个属性：Number.EPSILON 静态数据属性，表示 1 与大于 1 的最小浮点数之间的差值。

详细介绍可查看MDN (opens new window)。

我们对之前的代码做一些优化，在放大一定倍数之后，做差值比较，确认最终结果。

代码如下：

const getPower = (a, b, c) => {
  // 获取a,b小数位长度，如没有小数位则默认值为0
  const aLen = a.toString().split(".")[1]?.length || 0;
  const bLen = b.toString().split(".")[1]?.length || 0;
  const cLen = c.toString().split(".")[1]?.length || 0;
  // 获取最大长度
  const len = Math.max(aLen, bLen, cLen);
  // 计算返回放大倍数
  return Math.pow(10, len)
}
// 差值比价
const compare = (n) => {
  const result = Math.round(n);

  // 如差值小于 Number.EPSILON 则认为和取整之后的数字相等
  return n - result < Number.EPSILON ? result : n;
}

var a = 19.9;
var b = 4788.4;
var c = 0.01;
var power = getPower(a, b, c);

const result = (compare((a * power)) + compare((b * power)) + compare((c * power))) / power
console.log(result)

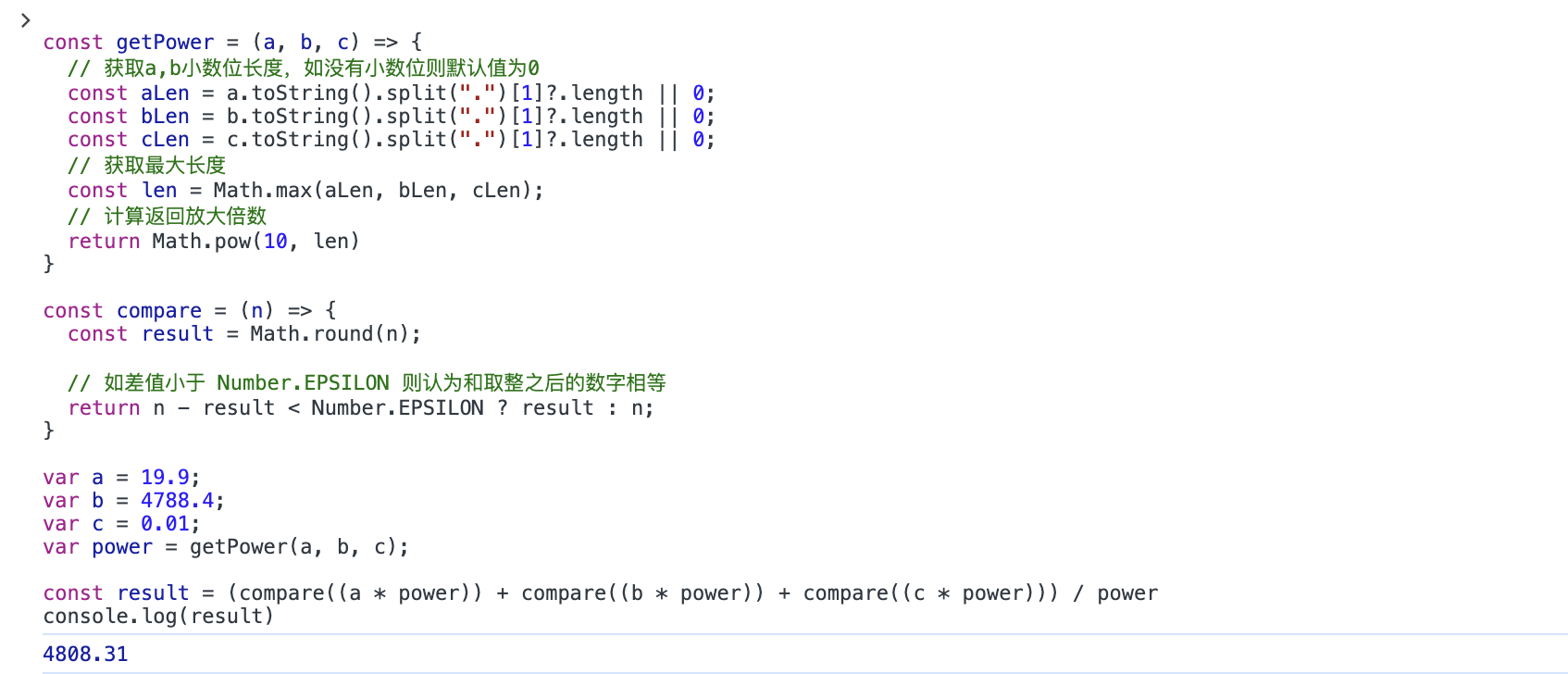
在浏览器运行代码，可知计算正确。

如下图所示：

# Math.round

理论上讲，一个两位小数乘 100 后一定会得到一个整数，一个三位小数乘 1000 以后一定也会得到一个整数。同理可知，一个 n 位小数乘（10^n）后，一定可以得到一个整数！

虽然在计算机世界中小数计算有些误差，但通过上述代码我们知道，这个误差小到几乎可以忽略，那么我们是不是可以大胆一点，放大之后无需比较，直接四舍五入！

我们修改以上代码，舍弃compare函数。

代码如下：

const getPower = (a, b, c) => {
  // 获取a,b小数位长度，如没有小数位则默认值为0
  const aLen = a.toString().split(".")[1]?.length || 0;
  const bLen = b.toString().split(".")[1]?.length || 0;
  const cLen = c.toString().split(".")[1]?.length || 0;
  // 获取最大长度
  const len = Math.max(aLen, bLen, cLen);
  // 计算返回放大倍数
  return Math.pow(10, len)
}

var a = 19.9;
var b = 4788.4;
var c = 0.01;
var power = getPower(a, b, c);

const result = (Math.round((a * power)) + Math.round((b * power)) + Math.round((c * power))) / power
console.log(result)

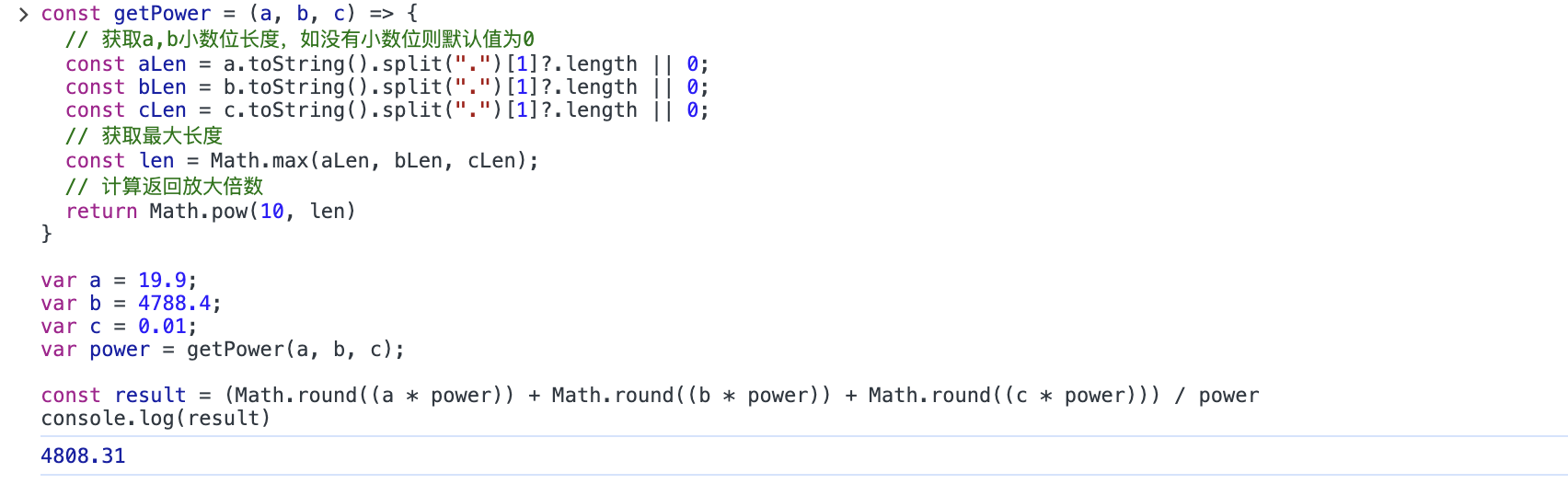
在浏览器中运行后发现，结果依然正确。

如下图所示：

# 封装完善

基于以上推导，我们可以封装一个简易的计算函数。

代码如下：

function compute(type, ...args) {
  // 计算放大倍数
  const getPower = (numbers) => {
    const lens = numbers.map(num => num.toString().split(".")[1]?.length || 0);
    // 获取最大长度
    const len = Math.max(...lens);
    // 计算返回放大倍数
    return Math.pow(10, len)
  }

  // 获取放大倍数
  const power = getPower(args);

  // 获取放大后的值
  const newNumbers = args.map(num => Math.round(num * power));

  // 计算结果
  let result = 0;
  switch (type) {
    case "+":
      result = newNumbers.reduce((preNumber, nextNumber) => preNumber + nextNumber, result) / power;
      break;
    case "-":
      result = newNumbers.reduce((preNumber, nextNumber) => preNumber - nextNumber) / power;
      break;
    case "*":
      result = newNumbers.reduce((preNumber, nextNumber) => preNumber * nextNumber) / (power ** newNumbers.length);
      break;
    case "/":
      result = newNumbers.reduce((preNumber, nextNumber) => preNumber / nextNumber);
      break;
  }

  return {
    result,
    next(nextType, ...nextArgs) {
      return compute(nextType, result, ...nextArgs);
    }
  }
}

// 验证
const arr = [0.1, 0.2, 29.6]
const a = compute('+', ...arr);
const b = a.next('-', 4, 2, 4);
const c = b.next('*', 100);
const d = c.next('+', 2798.4);
const e = d.next('*', 100);
const f = e.next('/', 1000);
const r = compute('+', ...arr).next('-', 4, 2, 4).next('*', 100).next('+', 2798.4).next('*', 100).next('/', 1000);

console.log('a: ', a.result) // a:  29.9
console.log('b: ', b.result) // b:  19.9
console.log('c: ', c.result) // c:  1990
console.log('d: ', d.result) // d:  4788.4
console.log('e: ', e.result) // e:  478840
console.log('f: ', f.result) // f:  478.84
console.log('r: ', r.result) // f:  478.84

经简单测试后，可知compute函数已实现基本的四则运算，且可以链式调用。

# 结语

若有错误，请务必给予指正。谢谢！

# 参考文档

Number.EPSILON (opens new window)

一份自动部署VuePress到GithubPages的脚本

凡铁的博客

Choose mode